Correlation Between Categorical Variable and Continuous Variable in Sas
This page is archived and no longer maintained.
Chapter Outline
1. Continuous and categorical predictors without interaction
2. Continuous and categorical predictors with interaction
3. Show slopes for each group
3.1 Show slopes by performing separate analyses
3.2 Show slopes for each group from one analysis
4. Compare slopes across groups
5. Simple effects and simple comparisons of group, strategy 1
5.1 Simple effects and comparisons when meals is 1 sd below mean
5.2 Simple effects and comparisons when meals is at the mean
5.3 Simple effects and comparisons when meals is 1 sd above the mean
6. Simple effects and simple comparisons of group, strategy 2
7. More on predicted values
1.0 Continuous and categorical predictors without interaction
data elemapi2; set 'd:sassasdataelemapi2'; run;
Creating the variables Icollcat2 and Icollcat3 by using the reverse Helmert coding on collcat.
Table of Icollcat2 by collcat Frequency| 1| 2| 3| Total ———+——–+——–+——–+ -0.5 | 129 | 0 | 0 | 129 ———+——–+——–+——–+ 0 | 0 | 0 | 137 | 137 ———+——–+——–+——–+ 0.5 | 0 | 134 | 0 | 134 ———+——–+——–+——–+ Total 129 134 137 400 Frequency | 1| 2| 3| Total ————-+——–+——–+——–+ -0.333333333 | 129 | 134 | 0 | 263 ————-+——–+——–+——–+ 0.6666666667 | 0 | 0 | 137 | 137 ————-+——–+——–+——–+ Total 129 134 137 400
data elemapi2; set elemapi2; Icollcat2 = 0; if collcat = 1 then Icollcat2 = -.5; if collcat = 2 then Icollcat2 = .5; Icollcat3 = 2/3; if collcat = 1 then Icollcat3 = -1/3; if collcat = 2 then Icollcat3 = -1/3; run; proc freq data=elemapi2; tables ( Icollcat2 Icollcat3)*collcat/ norow nocol nopercent ; run;
The FREQ Procedure
Icollcat2 collcat
Table of Icollcat3 by collcat
Icollcat3 collcat
Traditional ANCOVA: regressing a continuous dependent variable on predictors that includes both categorical and
continuous predictors (without any interactions).
Analysis of Variance Sum of Mean Source DF Squares Square F Value Pr > F Root MSE 61.27270 R-Square 0.8159 Dependent Mean 647.62250 Adj R-Sq 0.8145 Coeff Var 9.46118 Parameter Standard Variable DF Estimate Error t Value Pr > |t|
proc reg data= elemapi2; model api00 = Icollcat2 Icollcat3 meals; output out=temp p=predict; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: api00 api 2000
Model 3 6586952 2195651 584.83 <.0001 Error 396 1486720 3754.34394 Corrected Total 399 8073672
Parameter Estimates
Intercept 1 885.17891 6.71886 131.75 <.0001 Icollcat2 1 14.01454 7.62786 1.84 0.0669 Icollcat3 1 17.23322 6.58145 2.62 0.0092 meals 1 -3.94267 0.09883 -39.89 <.0001
Generating the graph with a regression line for each level of collcat.
Note: Each line has the same slope, namely the coefficient of meals in the regression output. The coefficient of
Icollcat2 is the difference in y-intercepts between the lines for collcat=1 and collcat=2 whereas the coefficient of
Icollcat3 is the difference in y-intercept between the line for collcat=3 and the average of the lines for collcat=1
and collcat=2. This is simply a result of using the reverse Helmert coding for collcat when creating Icollcat2 and
Icollcat3.
goptions reset=all; symbol1 v=square i=join c=blue h=.6; symbol2 v=dot i=join c=red h=.6; symbol3 v=plus i=join c=green h=.6; axis1 label=(a=90 'Predicted'); proc gplot data=temp; plot predict*meals=collcat/overlay vaxis=axis1; run; quit;
2.0 Continuous and categorical predictors with interaction
Testing the homogeneity of slopes by creating the two interactions and then testing to see if the overall
interaction is significant.
Analysis of Variance Sum of Mean Source DF Squares Square F Value Pr > F Root MSE 60.53363 R-Square 0.8212 Dependent Mean 647.62250 Adj R-Sq 0.8189 Coeff Var 9.34705 Parameter Standard Variable DF Estimate Error t Value Pr > |t| Test interaction Results for Dependent Variable api00 Mean Source DF Square F Value Pr > F
data elemapi2; set elemapi2; Icolmeal2 = Icollcat2*meals; Icolmeal3 = Icollcat3*meals; run; proc reg data=elemapi2; model api00 = meals Icollcat2 Icollcat3 Icolmeal2 Icolmeal3; output out=temp p=predict; interaction: test Icolmeal2=Icolmeal3=0; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: api00 api 2000
Model 5 6629930 1325986 361.86 <.0001 Error 394 1443742 3664.32012 Corrected Total 399 8073672
Parameter Estimates
Intercept 1 882.47026 6.69004 131.91 <.0001 meals 1 -3.85935 0.10064 -38.35 <.0001 Icollcat2 1 10.29492 16.24717 0.63 0.5267 Icollcat3 1 -26.42920 14.31193 -1.85 0.0655 Icolmeal2 1 0.02815 0.22250 0.13 0.8994 Icolmeal3 1 0.79489 0.23242 3.42 0.0007
The REG Procedure Model: MODEL1
Numerator 2 21489 5.86 0.0031 Denominator 394 3664.32012
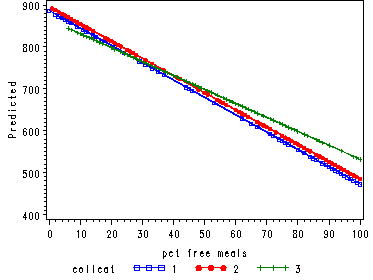
Generating a graph with a regression line for each of the levels of collcat.
Note: The lines are no longer parallel like they were in the previous graph which we
expected to see since the overall interaction test was significant.
goptions reset=all; symbol1 v=square i=join c=blue h=.6; symbol2 v=dot i=join c=red h=.6; symbol3 v=plus i=join c=green h=.6; axis1 label=(a=90 'Predicted'); proc gplot data=temp; plot predict*meals = collcat/overlay vaxis=axis1; run; quit;
3.0 Show slopes for each group
3.1 Show slopes by performing separate analyses
It is entirely possible to get the slope and y-intercept for the regression line for each of
the levels of collcat. The by statement in the regression will accomplish this very easily.
Note: We need to sort the data set on collcat before we can use the by statement.
Analysis of Variance Sum of Mean Source DF Squares Square F Value Pr > F Root MSE 62.76483 R-Square 0.8395 Dependent Mean 596.34884 Adj R-Sq 0.8383 Coeff Var 10.52485 Parameter Standard Variable DF Estimate Error t Value Pr > |t| Analysis of Variance Sum of Mean Source DF Squares Square F Value Pr > F Root MSE 59.86411 R-Square 0.8368 Dependent Mean 651.50000 Adj R-Sq 0.8355 Coeff Var 9.18866 Parameter Standard Variable DF Estimate Error t Value Pr > |t| Sum of Mean Source DF Squares Square F Value Pr > F Root MSE 59.02827 R-Square 0.6747 Dependent Mean 692.10949 Adj R-Sq 0.6723 Coeff Var 8.52875 Parameter Standard Variable DF Estimate Error t Value Pr > |t|
proc sort data=elemapi2 out=elemapisort; by collcat; run; proc reg data=elemapisort; by collcat; model api00=meals; run; quit;
collcat=1
The REG Procedure Model: MODEL1 Dependent Variable: api00 api 2000
Model 1 2617393 2617393 664.41 <.0001 Error 127 500307 3939.42342 Corrected Total 128 3117699
Parameter Estimates
Intercept 1 886.13253 12.52709 70.74 <.0001 meals 1 -4.13839 0.16055 -25.78 <.0001
collcat=2
Model 1 2424782 2424782 676.61 <.0001 Error 132 473050 3583.71194 Corrected Total 133 2897832
Parameter Estimates
Intercept 1 896.42745 10.74270 83.45 <.0001 meals 1 -4.11024 0.15801 -26.01 <.0001
collcat=3 Analysis of Variance
Model 1 975466 975466 279.96 <.0001 Error 135 470385 3484.33611 Corrected Total 136 1445851
Parameter Estimates
Intercept 1 864.85079 11.48996 75.27 <.0001 meals 1 -3.32943 0.19899 -16.73 <.0001
3.2 Obtaining slopes for each group in one analysis
Obtaining the slope of meals for each level of collcat by first sorting the data and then using a by statement can be a bit cumbersome. Instead we can use the estimate statement in proc glm. Recall the variable coded using the reverse Helmert coding:
collcat Icollcat2 Icollcat3 1 -.5 -1/3 2 .5 -1/3 3 0 -2/3
Thus, in order to get the slope of meals we need to have the appropriate coefficient for each of the interaction variables. For example, for the collcat=1 group the coefficient for Icolmeal2 will be the coefficient in the column for Icollcat2 in the collcat=1 row in the table above. In other words, the coefficient for Icolmeal2 will be -.5. This is because Icolmeal2 is the interaction of Icollcat2 and meals. Using the same logic we find that the coefficient for Icolmeal3 is -1/3, the coefficient for Icollcat3 in the collcat=1 row in the table above. Furthermore, using the same reasoning we find that for the collcat=2 group the coefficient for Icolmeal2 is .5 and for Icolmeal3 the coefficient is -1/3. For the collcat=3 group the coefficient for
Icolmeal2 is 0 and for Icolmeal3 it is -2/3.
Note: We are using the regression coding and the proc glm is missing a class statement which means that proc glm is basically functioning as a proc reg–but it is a new an improved proc reg because now it has an estimate statement!!!! Dependent Variable: api00 api 2000 Sum of Source DF Squares Mean Square F Value Pr > F Obtaining the exact same results using the GLM default coding (and a class statement so that proc glm functions Class Level Information Class Levels Values Number of observations 400 The GLM Procedure Dependent Variable: api00 api 2000 Sum of Source DF Squares Mean Square F Value Pr > F 4.0 Comparing Slopes Across Groups Analysis of Variance Sum of Mean Source DF Squares Square F Value Pr > F Root MSE 60.53363 R-Square 0.8212 Dependent Mean 647.62250 Adj R-Sq 0.8189 Coeff Var 9.34705 Parameter Standard Variable DF Estimate Error t Value Pr > |t| 5.0 Simple Effects and Simple Comparisons of Groups, method I The tests of the coefficients of the interactions reflect if the slopes of the groups are 5.1 Simple effects and comparisons when meals = means – 1std. Now that we have the new variable for meals we can perform the same regression as previously and the Analysis of Variance Sum of Mean Source DF Squares Square F Value Pr > F Root MSE 60.53363 R-Square 0.8212 Dependent Mean 647.62250 Adj R-Sq 0.8189 Coeff Var 9.34705 Parameter Standard Variable DF Estimate Error t Value Pr > |t| Test test Results for Dependent Variable api00 Mean Source DF Square F Value Pr > F By looking at the coefficient for Icollcat2 in the regression output we can see if the simple comparison of the group collcat=1 and the group collcat=2 is significant. The t-test has a p-value of 0.316 and this comparison is therefore not statistically significant at the 0.05 level. We can see if the simple comparison of groups 3 vs group 12 is significant by looking at the coefficient for Icollcat3. We can also calculate these numbers by recalling that Icollcat2 is the difference in the y-intercept between groups 1 and 2. Let's calculate the predicted values (y-intercepts) for group 1 and for group 2 using proc glm and then we can subtract them to get exactly the coefficient for Icollcat2. We will also obtain the test of the simple comparison between group 3 and groups 1,2, as well as the predicted values for groups 12 and 3 at meals=28.4 (one standard deviation below the mean). Note: We are using the regression coding and the proc glm is missing a class statement which means that proc glm is basically functioning as a proc reg–but it is a new an improved proc reg because now it has an estimate statement!!!! Dependent Variable: api00 api 2000 Sum of Source DF Squares Mean Square F Value Pr > F Class Level Information Class Levels Values Number of observations 400 The GLM Procedure Dependent Variable: api00 api 2000 Sum of Source DF Squares Mean Square F Value Pr > F
proc glm data=elemapi2; model api00 = meals Icollcat2 Icollcat3 Icolmeal2 Icolmeal3; estimate 'slope of meals at collcat=1' meals 1 Icolmeal2 -.5 Icolmeal3 -.333333333; estimate 'slope of meals at collcat=2' meals 1 Icolmeal2 .5 Icolmeal3 -.3333333333; estimate 'slope of meals at collcat=3' meals 1 Icolmeal2 0 Icolmeal3 .666666667; run; quit;
The GLM Procedure Number of observations 400 The GLM Procedure
Model 5 6629929.872 1325985.974 361.86 <.0001 Error 394 1443742.126 3664.320 Corrected Total 399 8073671.998
R-Square Coeff Var Root MSE api00 Mean
0.821179 9.347054 60.53363 647.6225
Source DF Type I SS Mean Square F Value Pr > F
meals 1 6549825.145 6549825.145 1787.46 <.0001 Icollcat2 1 11385.768 11385.768 3.11 0.0787 Icollcat3 1 25740.884 25740.884 7.02 0.0084 Icolmeal2 1 115.990 115.990 0.03 0.8589 Icolmeal3 1 42862.086 42862.086 11.70 0.0007
Source DF Type III SS Mean Square F Value Pr > F
meals 1 5389132.969 5389132.969 1470.70 <.0001 Icollcat2 1 1471.242 1471.242 0.40 0.5267 Icollcat3 1 12495.833 12495.833 3.41 0.0655 Icolmeal2 1 58.655 58.655 0.02 0.8994 Icolmeal3 1 42862.086 42862.086 11.70 0.0007
Standard Parameter Estimate Error t Value Pr > |t|
slope of meals at collcat=1 -4.13839216 0.15484383 -26.73 <.0001 slope of meals at collcat=2 -4.11024157 0.15978196 -25.72 <.0001 slope of meals at collcat=3 -3.32942579 0.20406098 -16.32 <.0001
Standard Parameter Estimate Error t Value Pr > |t|
Intercept 882.4702589 6.69003553 131.91 <.0001 meals -3.8593532 0.10063563 -38.35 <.0001 Icollcat2 10.2949246 16.24717093 0.63 0.5267 Icollcat3 -26.4292002 14.31192705 -1.85 0.0655 Icolmeal2 0.0281506 0.22250143 0.13 0.8994 Icolmeal3 0.7948911 0.23241688 3.42 0.0007
as proc glm and not as a proc reg).
proc glm data=elemapi2; class collcat; model api00 = meals collcat collcat*meals ; estimate 'slope of meals at collcat=1' meals 1 collcat*meals 1 0 0; estimate 'slope of meals at collcat=2' meals 1 collcat*meals 0 1 0; estimate 'slope of meals at collcat=3' meals 1 collcat*meals 0 0 1; run; quit;
The GLM Procedure
collcat 3 1 2 3
Model 5 6629929.872 1325985.974 361.86 <.0001 Error 394 1443742.126 3664.320 Corrected Total 399 8073671.998
R-Square Coeff Var Root MSE api00 Mean
0.821179 9.347054 60.53363 647.6225
Source DF Type I SS Mean Square F Value Pr > F
meals 1 6549825.145 6549825.145 1787.46 <.0001 collcat 2 37126.652 18563.326 5.07 0.0067 meals*collcat 2 42978.076 21489.038 5.86 0.0031
Source DF Type III SS Mean Square F Value Pr > F
meals 1 5389132.969 5389132.969 1470.70 <.0001 collcat 2 14535.351 7267.676 1.98 0.1390 meals*collcat 2 42978.076 21489.038 5.86 0.0031
Standard Parameter Estimate Error t Value Pr > |t|
slope of meals at collcat=1 -4.13839216 0.15484383 -26.73 <.0001 slope of meals at collcat=2 -4.11024157 0.15978196 -25.72 <.0001 slope of meals at collcat=3 -3.32942579 0.20406098 -16.32 <.0001
By using the reverse Helmert coding we can compare slopes of group 1 versus group2
by looking at the t-test for the coefficient of Icolmeal2. We can compare the slopes of
group 3 versus the average of groups 1 and 2 by looking at the t-test for the coefficient
of Icolmeal2 and Icolmeal3. From this we can conclude that the slopes of groups 1 and 2 are not
significantly different (p=0.8994) but that the slope of group 3 is significantly different
from the slope of the average of groups 1 and 2 (p=0.0007).
proc reg data=elemapi2; model api00 = meals Icollcat2 Icollcat3 Icolmeal2 Icolmeal3; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: api00 api 2000
Model 5 6629930 1325986 361.86 <.0001 Error 394 1443742 3664.32012 Corrected Total 399 8073672
Parameter Estimates
Intercept 1 882.47026 6.69004 131.91 <.0001 meals 1 -3.85935 0.10064 -38.35 <.0001 Icollcat2 1 10.29492 16.24717 0.63 0.5267 Icollcat3 1 -26.42920 14.31193 -1.85 0.0655 Icolmeal2 1 0.02815 0.22250 0.13 0.8994 Icolmeal3 1 0.79489 0.23242 3.42 0.0007
significantly different across the whole dataset. However, sometimes it can be very
informative to test for significant difference between the groups at specific points in the
dataset. A common strategy is to test for differences at the mean, the mean – 1 standard
deviation, the mean + 1 standard deviation. So, we need to calculate the mean and
standard deviation of meals.
Here we insert the graph maybe with circles and/or moving parts!
proc means data=elemapi2 mean std; var meals; run; proc reg data=elemapi2 noprint; model api00 = meals Icollcat2 Icollcat3 Icolmeal2 Icolmeal3; output out=temp p=predict; run; quit; goptions reset=all; symbol1 v=square i=join c=blue h=.6; symbol2 v=dot i=join c=red h=.6; symbol3 v=plus i=join c=green h=.6; axis1 label=(a=90 'Predicted'); axis2 label=(' '); proc gplot data=temp; plot predict*meals=collcat/overlay vaxis=axis1 haxis=axis2 href=28.403299 60.3150000 92.226701; run; quit; The MEANS Procedure Analysis Variable : meals pct free meals Mean Std Dev ---------------------------- 60.3150000 31.9117011 ----------------------------
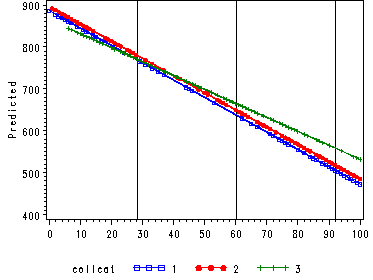
First, we generate a variable for meals that is shifted to be centered at one standard
deviation below the mean using proc sql. We also create new interaction variables
using the new variable for meals.
proc sql; create table low as select *, meals - ( mean(meals) - std(meals) ) as meals_low from elemapi2; quit; data low; set low; Icolmeals2_low = Icollcat2*meals_low; Icolmeals3_low = Icollcat3*meals_low; run;
only difference is that instead of meals we will use meals_low. By using the variable for meals centered
at one standard deviation below the mean we can now test for group differences at this specific point.
If you refer to the graph above we are testing for group differences at the first vertical line. Since the
three lines are very close together we anticipate that we probably won't find any significant differences.
proc reg data=low; model api00 = meals_low Icollcat2 Icollcat3 Icolmeals2_low Icolmeals3_low; test: test Icollcat2=Icollcat3=0; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: api00 api 2000
Model 5 6629930 1325986 361.86 <.0001 Error 394 1443742 3664.32012 Corrected Total 399 8073672
Parameter Estimates
Intercept 1 772.85190 4.36931 176.88 <.0001 meals_low 1 -3.85935 0.10064 -38.35 <.0001 Icollcat2 1 11.09449 11.05054 1.00 0.3160 Icollcat3 1 -3.85167 8.95725 -0.43 0.6674 Icolmeals2_low 1 0.02815 0.22250 0.13 0.8994 Icolmeals3_low 1 0.79489 0.23242 3.42 0.0007
Numerator 2 2346.37142 0.64 0.5277 Denominator 394 3664.32012
proc glm data=low; model api00 = meals_low Icollcat2 Icollcat3 Icolmeals2_low Icolmeals3_low; estimate 'simple comparisons group 1 v 2, m=28.4' Icollcat2 1; estimate 'predicted value group 1, m=28.4' intercept 1 Icollcat2 -.5 Icollcat3 -.3333333; estimate 'predicted value group 2, m=28.4' intercept 1 Icollcat2 .5 Icollcat3 -.3333333; estimate 'simple comparisons group 3 vs 12, m=28.4' Icollcat3 1; estimate 'predicted value group 1,1, m=28.4' intercept 1 Icollcat2 0 Icollcat3 -.3333333; estimate 'predicted value group 2, m=28.4' intercept 1 Icollcat2 0 Icollcat3 .6666667; run; quit;
The GLM Procedure Number of observations 400 The GLM Procedure
Model 5 6629929.872 1325985.974 361.86 <.0001 Error 394 1443742.126 3664.320 Corrected Total 399 8073671.998
R-Square Coeff Var Root MSE api00 Mean
0.821179 9.347054 60.53363 647.6225
Source DF Type I SS Mean Square F Value Pr > F
meals_low 1 6549825.145 6549825.145 1787.46 <.0001 Icollcat2 1 11385.768 11385.768 3.11 0.0787 Icollcat3 1 25740.884 25740.884 7.02 0.0084 Icolmeals2_low 1 115.990 115.990 0.03 0.8589 Icolmeals3_low 1 42862.086 42862.086 11.70 0.0007
Source DF Type III SS Mean Square F Value Pr > F
meals_low 1 5389132.969 5389132.969 1470.70 <.0001 Icollcat2 1 3693.531 3693.531 1.01 0.3160 Icollcat3 1 677.552 677.552 0.18 0.6674 Icolmeals2_low 1 58.655 58.655 0.02 0.8994 Icolmeals3_low 1 42862.086 42862.086 11.70 0.0007
Standard Parameter Estimate Error t Value Pr > |t|
comparisons group 1 v 2, m=28.4 11.094494 11.0505357 1.00 0.3160 pred value group 1, m=28.4 768.588540 8.3629162 91.90 <.0001 pred value group 2, m=28.4 779.683035 7.2232933 107.94 <.0001 comparisons group 3 vs 12, m=28.4 -3.851671 8.9572501 -0.43 0.6674 pred value group 1,1, m=28.4 774.135788 5.5252676 140.11 <.0001 pred value group 2, m=28.4 770.284116 7.0500883 109.26 <.0001
Standard Parameter Estimate Error t Value Pr > |t|
Intercept 772.8518972 4.36931324 176.88 <.0001 meals_low -3.8593532 0.10063563 -38.35 <.0001 Icollcat2 11.0944942 11.05053567 1.00 0.3160 Icollcat3 -3.8516714 8.95725011 -0.43 0.6674 Icolmeals2_low 0.0281506 0.22250143 0.13 0.8994 Icolmeals3_low 0.7948911 0.23241688 3.42 0.0007
Obtaining the exact same results using the GLM coding (and a class statement so that proc glm functions as proc glm and not as a proc reg). proc glm data=elemapi2; class collcat; model api00 = meals collcat collcat*meals ; estimate 'slope of 2 v 1 at m=28.4' collcat -1 1 0 collcat*meals -28.4 28.4 0; estimate 'pred values, group 1, m=28.4' intercept 1 meals 28.4 collcat 1 0 0 collcat*meals 28.4 0 0; estimate 'pred values, group 2, m=28.4' intercept 1 meals 28.4 collcat 0 1 0 collcat*meals 0 28.4 0; estimate 'pred values, group 12, m=28.4' intercept 1 meals 28.4 collcat .5 .5 0 collcat*meals 14.2 14.2 0; estimate 'pred values, group 3, m=28.4' intercept 1 meals 28.4 collcat 0 0 1 collcat*meals 0 0 28.4; estimate 'slope of 3 v 12 at m=28.4' collcat -.5 -.5 1 collcat*meals -14.2 -14.2 28.4; run; quit;
The GLM Procedure
collcat 3 1 2 3
Model 5 6629929.872 1325985.974 361.86 <.0001 Error 394 1443742.126 3664.320 Corrected Total 399 8073671.998
R-Square Coeff Var Root MSE api00 Mean
0.821179 9.347054 60.53363 647.6225
Source DF Type I SS Mean Square F Value Pr > F
meals 1 6549825.145 6549825.145 1787.46 <.0001 collcat 2 37126.652 18563.326 5.07 0.0067 meals*collcat 2 42978.076 21489.038 5.86 0.0031
Source DF Type III SS Mean Square F Value Pr > F
meals 1 5389132.969 5389132.969 1470.70 <.0001 collcat 2 14535.351 7267.676 1.98 0.1390 meals*collcat 2 42978.076 21489.038 5.86 0.0031
Standard Parameter Estimate Error t Value Pr > |t|
slope of 2 v 1 at m=28.4 11.094401 11.0510713 1.00 0.3160 pred values, group 1, m=28.4 768.602193 8.3633100 91.90 <.0001 pred values, group 2, m=28.4 779.696594 7.2236571 107.94 <.0001 pred values, group 12, m=28.4 774.149393 5.5255356 140.10 <.0001 pred values, group 3, m=28.4 770.295100 7.0505458 109.25 <.0001 slope of 3 v 12 at m=28.4 -3.854294 8.9577754 -0.43 0.6672
5.2 Simple Effects and Comparisons for meals=mean.
First, we generate a variable for meals that is shifted to be centered at the mean using proc sql. We also create new interaction variables
using the new variable for meals.
proc sql; create table mean as select *, meals - mean(meals) as meals_mean from elemapi2; quit; data mean; set mean; Icolmeals2_mean = Icollcat2*meals_mean; Icolmeals3_mean = Icollcat3*meals_mean; run;
Performing the regression using meals_mean and testing for the simple effects of collcat at meals=mean. Conclusion: The three groups of collcat are significantly different at meals=mean. The individual t-tests for Icollcat2 and Icollcat3, however, indicate that only the comparisons between group 3 and groups 1,2 is significant (p<.000).
Analysis of Variance Sum of Mean Source DF Squares Square F Value Pr > F Root MSE 60.53363 R-Square 0.8212 Dependent Mean 647.62250 Adj R-Sq 0.8189 Coeff Var 9.34705 Parameter Standard Variable DF Estimate Error t Value Pr > |t| Mean Source DF Square F Value Pr > F
proc reg data=mean; model api00=meals_mean Icollcat2 Icollcat3 Icolmeals2_mean Icolmeals3_mean; test: test Icollcat2=Icollcat3=0; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: api00 api 2000
Model 5 6629930 1325986 361.86 <.0001 Error 394 1443742 3664.32012 Corrected Total 399 8073672
Parameter Estimates
Intercept 1 649.69337 3.12218 208.09 <.0001 meals_mean 1 -3.85935 0.10064 -38.35 <.0001 Icollcat2 1 11.99283 7.61738 1.57 0.1162 Icollcat3 1 21.51465 6.64932 3.24 0.0013 Icolmeals2_mean 1 0.02815 0.22250 0.13 0.8994 Icolmeals3_mean 1 0.79489 0.23242 3.42 0.0007
Test test Results for Dependent Variable api00
Numerator 2 23138 6.31 0.0020 Denominator 394 3664.32012
Looking at the simple comparisons, first of group 1 vs 2 and then for group 3 vs 1,2 using proc glm.
Note: We are using the regression coding and the proc glm is missing a class statement which means that proc glm is basically functioning as a proc reg–but it is a new an improved proc reg because now it has an estimate statement!!!!
Dependent Variable: api00 api 2000 Sum of Source DF Squares Mean Square F Value Pr > F comparisons group 1 v 2, m=60.3 11.9928275 7.61738092 1.57 0.1162 comparisons group 3 vs 12, m=60.3 21.5146549 6.64931923 3.24 0.0013 Class Level Information Class Levels Values Number of observations 400 The GLM Procedure Dependent Variable: api00 api 2000 Sum of Source DF Squares Mean Square F Value Pr > F slope of 2 v 1 at m=60.3 11.992405 7.6178035 1.57 0.1162 slope of 3 v 12 at m=60.3 21.502731 6.6486489 3.23 0.0013
proc glm data=mean; model api00 =meals_mean Icollcat2 Icollcat3 Icolmeals2_mean Icolmeals3_mean; estimate 'simple comparisons group 1 v 2, m=60.3' Icollcat2 1; estimate 'simple comparisons group 3 vs 12, m=60.3' Icollcat3 1; run; quit;
The GLM Procedure Number of observations 400 The GLM Procedure
Model 5 6629929.872 1325985.974 361.86 <.0001 Error 394 1443742.126 3664.320 Corrected Total 399 8073671.998
R-Square Coeff Var Root MSE api00 Mean 0.821179 9.347054 60.53363 647.6225
Source DF Type I SS Mean Square F Value Pr > F
meals_mean 1 6549825.145 6549825.145 1787.46 <.0001 Icollcat2 1 11385.768 11385.768 3.11 0.0787 Icollcat3 1 25740.884 25740.884 7.02 0.0084 Icolmeals2_mean 1 115.990 115.990 0.03 0.8589 Icolmeals3_mean 1 42862.086 42862.086 11.70 0.0007
Source DF Type III SS Mean Square F Value Pr > F
meals_mean 1 5389132.969 5389132.969 1470.70 <.0001 Icollcat2 1 9082.915 9082.915 2.48 0.1162 Icollcat3 1 38362.580 38362.580 10.47 0.0013 Icolmeals2_mean 1 58.655 58.655 0.02 0.8994 Icolmeals3_mean 1 42862.086 42862.086 11.70 0.0007
Standard Parameter Estimate Error t Value Pr > |t|
Standard Parameter Estimate Error t Value Pr > |t|
Intercept 649.6933723 3.12217544 208.09 <.0001 meals_mean -3.8593532 0.10063563 -38.35 <.0001 Icollcat2 11.9928275 7.61738092 1.57 0.1162 Icollcat3 21.5146549 6.64931923 3.24 0.0013 Icolmeals2_mean 0.0281506 0.22250143 0.13 0.8994 Icolmeals3_mean 0.7948911 0.23241688 3.42 0.0007
Obtaining the exact same results using the GLM coding (and a class statement so that proc glm functions as proc glm and not as a proc reg).
proc glm data=elemapi2; class collcat; model api00 = meals collcat collcat*meals ; estimate 'slope of 2 v 1 at m=60.3' collcat -1 1 0 collcat*meals -60.3 60.3 0; estimate 'slope of 3 v 12 at m=60.3' collcat -.5 -.5 1 collcat*meals -30.15 -30.15 60.3; run; quit;
The GLM Procedure
collcat 3 1 2 3
Model 5 6629929.872 1325985.974 361.86 <.0001 Error 394 1443742.126 3664.320 Corrected Total 399 8073671.998
R-Square Coeff Var Root MSE api00 Mean
0.821179 9.347054 60.53363 647.6225
Source DF Type I SS Mean Square F Value Pr > F
meals 1 6549825.145 6549825.145 1787.46 <.0001 collcat 2 37126.652 18563.326 5.07 0.0067 meals*collcat 2 42978.076 21489.038 5.86 0.0031
Source DF Type III SS Mean Square F Value Pr > F
meals 1 5389132.969 5389132.969 1470.70 <.0001 collcat 2 14535.351 7267.676 1.98 0.1390 meals*collcat 2 42978.076 21489.038 5.86 0.0031
Standard Parameter Estimate Error t Value Pr > |t|
5.3 Simple Effects and Comparisons when Meals=mean+1 std
First, we generate a variable for meals that is shifted to be centered at one standard deviation above the mean using proc sql. We also create new interaction variables using the new variable for meals.
proc sql; create table high as select *, meals - ( mean(meals) + std(meals) ) as meals_high from elemapi2; quit; data high; set high; Icolmeals2_high = Icollcat2*meals_high; Icolmeals3_high = Icollcat3*meals_high; run;
Performing the regression using meals_mean and testing for the simple effects of collcat at meals=mean. Conclusion: The three groups of collcat are significantly different at meals=mean. The individual t-tests for Icollcat2 and Icollcat3 however indicate that only the comparison between group 3 and groups 1,2 is significant (p<.000).
Analysis of Variance Sum of Mean Source DF Squares Square F Value Pr > F Root MSE 60.53363 R-Square 0.8212 Dependent Mean 647.62250 Adj R-Sq 0.8189 Coeff Var 9.34705 Parameter Standard Variable DF Estimate Error t Value Pr > |t|
proc reg data=high; model api00 =meals_high Icollcat2 Icollcat3 Icolmeals2_high Icolmeals3_high; test: test Icollcat2=Icollcat3=0; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: api00 api 2000
Model 5 6629930 1325986 361.86 <.0001 Error 394 1443742 3664.32012 Corrected Total 399 8073672
Parameter Estimates
Intercept 1 526.53485 4.58606 114.81 <.0001 meals_high 1 -3.85935 0.10064 -38.35 <.0001 Icollcat2 1 12.89116 9.73478 1.32 0.1862 Icollcat3 1 46.88098 10.87258 4.31 <.0001 Icolmeals2_high 1 0.02815 0.22250 0.13 0.8994 Icolmeals3_high 1 0.79489 0.23242 3.42 0.0007
Test test Results for Dependent Variable api00 Mean Source DF Square F Value Pr > F
Numerator 2 38869 10.61 <.0001 Denominator 394 3664.32012
Looking at the simple comparisons, first of group 1 vs 2 and then for group 3 vs 1,2 using proc glm.
Note: We are using the regression coding and the proc glm is missing a class statement which means that proc glm is basically functioning as a proc reg–but it is a new an improved proc reg because now it has an estimate statement!!!!
Sum of Source DF Squares Mean Square F Value Pr > F Class Level Information Class Levels Values Number of observations 400 The GLM Procedure Dependent Variable: api00 api 2000 Sum of Source DF Squares Mean Square F Value Pr > F
proc glm data=high; model api00 =meals_high Icollcat2 Icollcat3 Icolmeals2_high Icolmeals3_high; estimate 'simple comparisons group 1 v 2, m=92.2' Icollcat2 1; estimate 'simple comparisons group 3 vs 12, m=92.2' Icollcat3 1; run; quit;
The GLM Procedure Number of observations 400 The GLM Procedure Dependent Variable: api00 api 2000
Model 5 6629929.872 1325985.974 361.86 <.0001 Error 394 1443742.126 3664.320 Corrected Total 399 8073671.998
R-Square Coeff Var Root MSE api00 Mean
0.821179 9.347054 60.53363 647.6225
Source DF Type I SS Mean Square F Value Pr > F
meals_high 1 6549825.145 6549825.145 1787.46 <.0001 Icollcat2 1 11385.768 11385.768 3.11 0.0787 Icollcat3 1 25740.884 25740.884 7.02 0.0084 Icolmeals2_high 1 115.990 115.990 0.03 0.8589 Icolmeals3_high 1 42862.086 42862.086 11.70 0.0007
Source DF Type III SS Mean Square F Value Pr > F
meals_high 1 5389132.969 5389132.969 1470.70 <.0001 Icollcat2 1 6425.767 6425.767 1.75 0.1862 Icollcat3 1 68127.391 68127.391 18.59 <.0001 Icolmeals2_high 1 58.655 58.655 0.02 0.8994 Icolmeals3_high 1 42862.086 42862.086 11.70 0.0007
Standard Parameter Estimate Error t Value Pr > |t|
comparisons group 1 v 2, m=92.2 12.8911608 9.7347822 1.32 0.1862 comparisons group 3 vs 12, m=92.2 46.8809811 10.8725776 4.31 <.0001
Standard Parameter Estimate Error t Value Pr > |t|
Intercept 526.5348475 4.58605897 114.81 <.0001 meals_high -3.8593532 0.10063563 -38.35 <.0001 Icollcat2 12.8911608 9.73478216 1.32 0.1862 Icollcat3 46.8809811 10.87257762 4.31 <.0001 Icolmeals2_high 0.0281506 0.22250143 0.13 0.8994 Icolmeals3_high 0.7948911 0.23241688 3.42 0.0007
Obtaining the exact same results using the GLM coding (and a class statement so that proc glm functions as proc glm and not as a proc reg).
proc glm data=elemapi2; class collcat; model api00 = meals collcat collcat*meals ; estimate 'slope of 2 v 1 at m=92.2' collcat -1 1 0 collcat*meals -92.2 92.2 0; estimate 'slope of 3 v 12 at m=92.2' collcat -.5 -.5 1 collcat*meals -46.1 -46.1 92.2; run; quit;
The GLM Procedure
collcat 3 1 2 3
Model 5 6629929.872 1325985.974 361.86 <.0001 Error 394 1443742.126 3664.320 Corrected Total 399 8073671.998
R-Square Coeff Var Root MSE api00 Mean
0.821179 9.347054 60.53363 647.6225
Source DF Type I SS Mean Square F Value Pr > F
meals 1 6549825.145 6549825.145 1787.46 <.0001 collcat 2 37126.652 18563.326 5.07 0.0067 meals*collcat 2 42978.076 21489.038 5.86 0.0031
Source DF Type III SS Mean Square F Value Pr > F
meals 1 5389132.969 5389132.969 1470.70 <.0001 collcat 2 14535.351 7267.676 1.98 0.1390 meals*collcat 2 42978.076 21489.038 5.86 0.0031
Standard Parameter Estimate Error t Value Pr > |t|
slope of 2 v 1 at m=92.2 12.8904091 9.7310376 1.32 0.1860 slope of 3 v 12 at m=92.2 46.8597567 10.8676142 4.31 <.0001
6.0 Simple effects, simple group and interaction comparisons, strategy 2
How to get all the all these comparisons from both proc reg and proc glm. proc reg only has a test statement. That means it will not give the estimate for the effect we are interested, only the significance test. For that reason, we have to switch to proc glm using its estimate statement.
Note1: .5*28.403 = 14.2015 and (1/3)*28.403=9.4676667, and (2/3)*28.403=18.935333.
Note2: For the interactions it is much more confusing because you have to pre-calculate all the correct coefficients. For example, the first interaction you can use (1*Icollcat2+ 60.315*Icolmeal2) – (1*Icollcat + 28.403*Icolmeal2) whereas in proc glm you have to reduce that to 31.912*Icolmeal2 in order to use it in an estimate statement. If you repeat the variables SAS will only recognize it the first time you use a variable and ignore it the other times.
Note: We are using the regression coding and the proc glm is missing a class statement which means that proc glm is basically functioning as a proc reg–but it is a new an improved proc reg because now it has an estimate statement!!!!
Analysis of Variance Sum of Mean Source DF Squares Square F Value Pr > F Root MSE 60.53363 R-Square 0.8212 Dependent Mean 647.62250 Adj R-Sq 0.8189 Coeff Var 9.34705 Parameter Standard Variable DF Estimate Error t Value Pr > |t| Test low Results for Dependent Variable api00 Mean Source DF Square F Value Pr > F Mean Source DF Square F Value Pr > F Mean Source DF Square F Value Pr > F Dependent Variable: api00 api 2000 Sum of Source DF Squares Mean Square F Value Pr > F Standard Parameter Estimate Error t Value Pr > |t| Class Level Information Class Levels Values Number of observations 400 The GLM Procedure Dependent Variable: api00 api 2000 Sum of Source DF Squares Mean Square F Value Pr > F
proc reg data=elemapi2; model api00 = meals Icollcat2 Icollcat3 Icolmeal2 Icolmeal3; low: test Icollcat2+28.403*Icolmeal2=0, Icollcat3+28.403*Icolmeal3=0; mean: test Icollcat2+60.315*Icolmeal2=0, Icollcat3+60.315*Icolmeal3=0; high: test Icollcat2+92.23*Icolmeal2=0, Icollcat3+92.23*Icolmeal3=0; run; quit; proc glm data=elemapi2; model api00 = meals Icollcat2 Icollcat3 Icolmeal2 Icolmeal3; estimate 'Group 1 v 2, meals=28.403' Icollcat2 1 Icolmeal2 28.403; estimate 'Predicted values, Group 1, m=28.403' intercept 1 Icollcat2 -.5 Icollcat3 -.3333333 meals 28.403 Icolmeal2 -14.2015 Icolmeal3 -9.4676667; estimate 'Predicted values, Group 2, m=28.403' intercept 1 Icollcat2 .5 Icollcat3 -.3333333 meals 28.403 Icolmeal2 14.2015 Icolmeal3 -9.4676667; estimate 'Group 3 v 12, meals=28.403' Icollcat3 1 Icolmeal3 28.403; estimate 'Predicted values, Group 12, m=28.403' intercept 1 Icollcat2 0 Icollcat3 -.3333333 meals 28.403 Icolmeal2 0 Icolmeal3 -9.4676667; estimate 'Predicted values, Group 1, m=28.403' intercept 1 Icollcat2 0 Icollcat3 .6666666667 meals 28.403 Icolmeal2 0 Icolmeal3 18.935333; estimate 'Group 1 v 2, meals=60.315' Icollcat2 1 Icolmeal2 60.315; estimate 'Group 3 v 12, meals=60.315' Icollcat3 1 Icolmeal3 60.315; estimate 'Group 1 v 2, meals=92.23' Icollcat2 1 Icolmeal2 92.23; estimate 'Group 3 v 12, meals=92.23' Icollcat3 1 Icolmeal3 92.23; estimate 'Interaction: group 1 v 2, m=mean v m=mean+1std' Icolmeal2 31.912; estimate 'Interaction: group 3 v 12, m=mean v m=mean+1std' Icolmeal3 31.912; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: api00 api 2000
Model 5 6629930 1325986 361.86 <.0001 Error 394 1443742 3664.32012 Corrected Total 399 8073672
Parameter Estimates
Intercept 1 882.47026 6.69004 131.91 <.0001 meals 1 -3.85935 0.10064 -38.35 <.0001 Icollcat2 1 10.29492 16.24717 0.63 0.5267 Icollcat3 1 -26.42920 14.31193 -1.85 0.0655 Icolmeal2 1 0.02815 0.22250 0.13 0.8994 Icolmeal3 1 0.79489 0.23242 3.42 0.0007
Numerator 2 2346.39755 0.64 0.5277 Denominator 394 3664.32012
Test mean Results for Dependent Variable api00
Numerator 2 23138 6.31 0.0020 Denominator 394 3664.32012
Test high Results for Dependent Variable api00
Numerator 2 38869 10.61 <.0001 Denominator 394 3664.32012
The GLM Procedure Number of observations 400 The GLM Procedure
Model 5 6629929.872 1325985.974 361.86 <.0001 Error 394 1443742.126 3664.320 Corrected Total 399 8073671.998
R-Square Coeff Var Root MSE api00 Mean
0.821179 9.347054 60.53363 647.6225
Source DF Type I SS Mean Square F Value Pr > F
meals 1 6549825.145 6549825.145 1787.46 <.0001 Icollcat2 1 11385.768 11385.768 3.11 0.0787 Icollcat3 1 25740.884 25740.884 7.02 0.0084 Icolmeal2 1 115.990 115.990 0.03 0.8589 Icolmeal3 1 42862.086 42862.086 11.70 0.0007
Source DF Type III SS Mean Square F Value Pr > F
meals 1 5389132.969 5389132.969 1470.70 <.0001 Icollcat2 1 1471.242 1471.242 0.40 0.5267 Icollcat3 1 12495.833 12495.833 3.41 0.0655 Icolmeal2 1 58.655 58.655 0.02 0.8994 Icolmeal3 1 42862.086 42862.086 11.70 0.0007
Standard Parameter Estimate Error t Value Pr > |t|
Group 1 v 2, meals=28.403 11.094486 11.0505842 1.00 0.3160 Pred values, Group 1, m=28.403 768.589777 8.3629518 91.90 <.0001 Pred values, Group 2, m=28.403 779.684262 7.2233262 107.94 <.0001 Group 3 v 12, meals=28.403 -3.851909 8.9572977 -0.43 0.6674 Pred values, Group 12, m=28.403 774.137020 5.5252918 140.11 <.0001 Pred values, Group 1, m=28.403 770.285111 7.0501298 109.26 <.0001 Group 1 v 2, meals=60.315 11.992828 7.6173809 1.57 0.1162 Group 3 v 12, meals=60.315 21.514655 6.6493192 3.24 0.0013 Group 1 v 2, meals=92.23 12.891254 9.7352449 1.32 0.1862 Group 3 v 12, meals=92.23 46.883603 10.8731909 4.31 <.0001 Group 1 v 2, m=mean v m=mean+1std 0.898342 7.1004657 0.13 0.8994 Group 3 v 12, m=mean v m=mean+1std 25.366564 7.4168876 3.42 0.0007
Intercept 882.4702589 6.69003553 131.91 <.0001 meals -3.8593532 0.10063563 -38.35 <.0001 Icollcat2 10.2949246 16.24717093 0.63 0.5267 Icollcat3 -26.4292002 14.31192705 -1.85 0.0655 Icolmeal2 0.0281506 0.22250143 0.13 0.8994 Icolmeal3 0.7948911 0.23241688 3.42 0.0007
Obtaining the exact same results using the GLM coding (and a class statement so that proc glm functions as proc glm and not as a proc reg).
proc glm data=elemapi2; class collcat; model api00 = meals collcat collcat*meals ; estimate 'slope of 2 v 1 at m=28.4' collcat -1 1 0 collcat*meals -28.4 28.4 0; estimate 'pred values, group 1, m=28.4' intercept 1 meals 28.4 collcat 1 0 0 collcat*meals 28.4 0 0; estimate 'pred values, group 2, m=28.4' intercept 1 meals 28.4 collcat 0 1 0 collcat*meals 0 28.4 0; estimate 'slope of 3 v 12 at m=28.4' collcat -.5 -.5 1 collcat*meals -14.2 -14.2 28.4; estimate 'pred values, group 12, m=28.4' intercept 1 meals 28.4 collcat .5 .5 0 collcat*meals 14.2 14.2 0; estimate 'pred values, group 3, m=28.4' intercept 1 meals 28.4 collcat 0 0 1 collcat*meals 0 0 28.4; estimate 'slope of 2 v 1 at m=60.3' collcat -1 1 0 collcat*meals -60.3 60.3 0; estimate 'slope of 3 v 12 at m=60.3' collcat -.5 -.5 1 collcat*meals -30.15 -30.15 60.3; estimate 'slope of 2 v 1 at m=92.2' collcat -1 1 0 collcat*meals -92.2 92.2 0; estimate 'slope of 3 v 12 at m=92.2' collcat -.5 -.5 1 collcat*meals -46.1 -46.1 92.2; estimate 'slope of 2 v 1 at m=60.3 v m=28.4' collcat*meals -31.9 31.9 0; estimate 'slope of 3 v 12 at m=60.3 v m=28.4' collcat*meals -15.95 -15.95 31.9 ; run; quit;
The GLM Procedure
collcat 3 1 2 3
Model 5 6629929.872 1325985.974 361.86 <.0001 Error 394 1443742.126 3664.320 Corrected Total 399 8073671.998
R-Square Coeff Var Root MSE api00 Mean
0.821179 9.347054 60.53363 647.6225
Source DF Type I SS Mean Square F Value Pr > F
meals 1 6549825.145 6549825.145 1787.46 <.0001 collcat 2 37126.652 18563.326 5.07 0.0067 meals*collcat 2 42978.076 21489.038 5.86 0.0031
Source DF Type III SS Mean Square F Value Pr > F
meals 1 5389132.969 5389132.969 1470.70 <.0001 collcat 2 14535.351 7267.676 1.98 0.1390 meals*collcat 2 42978.076 21489.038 5.86 0.0031
Standard Parameter Estimate Error t Value Pr > |t|
slope of 2 v 1 at m=28.4 11.094401 11.0510713 1.00 0.3160 pred values, group 1, m=28.4 768.602193 8.3633100 91.90 <.0001 pred values, group 2, m=28.4 779.696594 7.2236571 107.94 <.0001 slope of 3 v 12 at m=28.4 -3.854294 8.9577754 -0.43 0.6672 pred values, group 12, m=28.4 774.149393 5.5255356 140.10 <.0001 pred values, group 3, m=28.4 770.295100 7.0505458 109.25 <.0001 slope of 2 v 1 at m=60.3 11.992405 7.6178035 1.57 0.1162 slope of 3 v 12 at m=60.3 21.502731 6.6486489 3.23 0.0013 slope of 2 v 1 at m=92.2 12.890409 9.7310376 1.32 0.1860 slope of 3 v 12 at m=92.2 46.859757 10.8676142 4.31 <.0001 slope of 2 v 1 at m=60.3 v m=28.4 0.898004 7.0977957 0.13 0.8994 slope of 3 v 12 at m=60.3 v m=28.4 25.357025 7.4140986 3.42 0.0007
7.0 More on Predicted Values
To be expanded!
Source: https://stats.oarc.ucla.edu/sas/webbooks/reg/chapter7/regression-with-saschapter-7-categorical-and-continuous-predictors-and-interactions/
0 Response to "Correlation Between Categorical Variable and Continuous Variable in Sas"
Post a Comment